Bij het versturen van informatie gaat nogal eens iets mis. Daarom zoeken informatici en wiskundigen naar codes die fouten kunnen verbeteren. Een ‘slangencode’ kan daarbij helpen. Loeky Haryanto promoveert 15 januari op nieuwe methodes om zulke slangencodes te vinden.
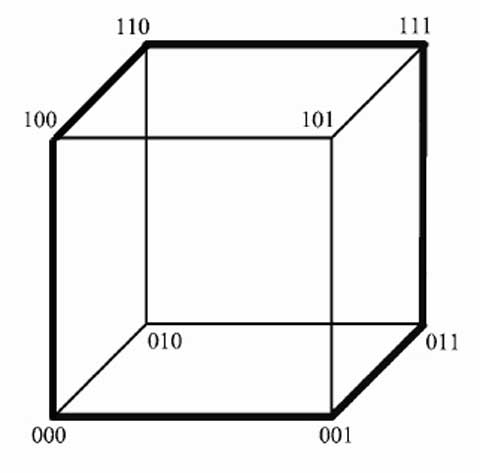
Computers en andere digitale apparaten slaan informatie op als binaire woorden: rijtjes van enen en nullen. Een slangencode is een lijst binaire woorden van dezelfde lengte . deze lengte heet de ‘dimensie’ van de code. Elke twee opeenvolgende woorden in de lijst verschillen precies op één plek. Bovendien moeten elke twee woorden die niet direct naast elkaar staan op minstens twee plekken verschillen. De slang bijt ook nog in zijn eigen staart, want het eerste en het laatste woord verschillen ook op precies één plaats. Een voorbeeld van zo’n slangencode in dimensie drie is 000, 001, 011, 111, 110, 100.
Slangen worden niet alleen gebruikt voor coderingen, er zijn ook toepassingen in computernetwerken en elektrotechniek. Voor de meeste toepassingen geldt: hoe langer de slang, hoe beter. Alleen zijn die lange slangen voor dimensies hoger dan zeven notoir moeilijk te vinden, doordat het aantal mogelijkheden explosief toeneemt. Vanaf dimensie acht is niet eens bekend wat de lengte is van de langst mogelijke slang.
“Krys Kochut van de Universiteit van Georgia wilde een lijst maken van alle langst denkbare slangen in de zevende dimensie”, vertelt promovendus Loeky Haryanto (afdeling toegepaste wiskunde, Elektrotechniek, Wiskunde en Informatica). “Vijf snelle computers moesten daarvoor meer dan een maand rekenen. Kochut vond uiteindelijk maar liefst 67.488 verschillende slangen. Maar vervolgens kon hij niet bewijzen dat hij ze nu ook allemaal gevonden had. Hij ging met dezelfde methode op zoek naar voorbeelden in de achtste dimensie. Toen vond hij precies één slang, waarvan hij echter weer niet kon bewijzen dat het ook echt de langst denkbare was. Dit soort resultaten geven aan dat het zoeken naar slangen in het algemeen een heel moeilijk probleem is.”
Vangen
Haryanto gebruikt een nieuwe methode om slangen te maken. Alle bestaande methodes werken met recursie: ze gebruiken kleinere slangen om de grotere te ‘vangen’. Om een slang in bijvoorbeeld zestien dimensies te vinden, heb je een slang in vijftien dimensies nodig. Die kleinere slang moet op de een of andere manier al eerder zijn gevonden.
Zo niet Haryanto: hij bouwt zijn slangen rechtstreeks vanaf een speciaal soort lineaire codes, zogenoemde ‘Reed-Muller-codes’. Daarmee kan hij in één stap slangen in 2, 4, 8, 16 of 32 dimensies maken. De woorden uit de Reed-Muller-code vormen de ruggengraat van de slang: elk vierde woord is afkomstig uit die code. “Een soortgelijke methode is eerder gebruikt door mijn promotor prof.dr. Jan van Zanten voor een ander probleem. We zijn de eersten die op deze manier slangen maken.”
Het voordeel van de aanpak van Haryanto is dat zijn slangen veel structuur meekrijgen van de onderliggende lineaire code. Daardoor kan hij ook kijken naar een andere vraag. Hoeveel slangen van dezelfde lengte zijn er eigenlijk nodig om alle verschillende woorden in een bepaalde dimensie te maken, zoals de twee (driedimensionale) slangen 000, 010, 011, 001 en 100, 101, 111, 110? De slangen mogen geen woorden gemeenschappelijk hebben.
Er was alleen bekend dat zulke ‘overdekkingen’ bestaan, maar een concrete constructie voor een willekeurige dimensie was nog niet bekend. Haryanto bracht daarin verandering: hij bewees dat elke lijst van 2^n-woorden kan worden overdekt met 2^{m-1}-slangen van dezelfde lengte, waarbij m bepaald wordt door te kijken tussen welke machten van twee n in ligt: 2^{m-1} < n < =2^{m}. Zodoende zijn er in het voorbeeld met de driedimensionale slangen twee slangen nodig van lengte 4.
Deze slangenoverdekkingen kunnen gebruikt worden voor efficiëntere codes. Het is namelijk een groot voordeel dat alle mogelijke woorden gebruikt kunnen worden. Haryanto verwacht dat zijn werk in de toekomst toepassingen zal vinden: “Er zijn zoveel toepassingen voor gewone slangencodes, dat ook deze overdekkingen nuttig zullen zijn. Maar ze zijn gloednieuw. En er zit altijd enige tijd tussen een wiskundige ontdekking en de praktische toepassing.”
De ‘slangencode’ dankt zijn naam aan een meetkundige interpretatie. Als je een kubus tekent en de hoekpunten binair nummert, dan vind je de slangencode door als een slang langs de ribben te kronkelen, met inachtneming van een spelregel: steeds als je op een nieuw hoekpunt aankomt, dan moet je het vorige hoekpunt en alle buurpunten daarvan als onbruikbaar markeren.
Computers en andere digitale apparaten slaan informatie op als binaire woorden: rijtjes van enen en nullen. Een slangencode is een lijst binaire woorden van dezelfde lengte . deze lengte heet de ‘dimensie’ van de code. Elke twee opeenvolgende woorden in de lijst verschillen precies op één plek. Bovendien moeten elke twee woorden die niet direct naast elkaar staan op minstens twee plekken verschillen. De slang bijt ook nog in zijn eigen staart, want het eerste en het laatste woord verschillen ook op precies één plaats. Een voorbeeld van zo’n slangencode in dimensie drie is 000, 001, 011, 111, 110, 100.
Slangen worden niet alleen gebruikt voor coderingen, er zijn ook toepassingen in computernetwerken en elektrotechniek. Voor de meeste toepassingen geldt: hoe langer de slang, hoe beter. Alleen zijn die lange slangen voor dimensies hoger dan zeven notoir moeilijk te vinden, doordat het aantal mogelijkheden explosief toeneemt. Vanaf dimensie acht is niet eens bekend wat de lengte is van de langst mogelijke slang.
“Krys Kochut van de Universiteit van Georgia wilde een lijst maken van alle langst denkbare slangen in de zevende dimensie”, vertelt promovendus Loeky Haryanto (afdeling toegepaste wiskunde, Elektrotechniek, Wiskunde en Informatica). “Vijf snelle computers moesten daarvoor meer dan een maand rekenen. Kochut vond uiteindelijk maar liefst 67.488 verschillende slangen. Maar vervolgens kon hij niet bewijzen dat hij ze nu ook allemaal gevonden had. Hij ging met dezelfde methode op zoek naar voorbeelden in de achtste dimensie. Toen vond hij precies één slang, waarvan hij echter weer niet kon bewijzen dat het ook echt de langst denkbare was. Dit soort resultaten geven aan dat het zoeken naar slangen in het algemeen een heel moeilijk probleem is.”
Vangen
Haryanto gebruikt een nieuwe methode om slangen te maken. Alle bestaande methodes werken met recursie: ze gebruiken kleinere slangen om de grotere te ‘vangen’. Om een slang in bijvoorbeeld zestien dimensies te vinden, heb je een slang in vijftien dimensies nodig. Die kleinere slang moet op de een of andere manier al eerder zijn gevonden.
Zo niet Haryanto: hij bouwt zijn slangen rechtstreeks vanaf een speciaal soort lineaire codes, zogenoemde ‘Reed-Muller-codes’. Daarmee kan hij in één stap slangen in 2, 4, 8, 16 of 32 dimensies maken. De woorden uit de Reed-Muller-code vormen de ruggengraat van de slang: elk vierde woord is afkomstig uit die code. “Een soortgelijke methode is eerder gebruikt door mijn promotor prof.dr. Jan van Zanten voor een ander probleem. We zijn de eersten die op deze manier slangen maken.”
Het voordeel van de aanpak van Haryanto is dat zijn slangen veel structuur meekrijgen van de onderliggende lineaire code. Daardoor kan hij ook kijken naar een andere vraag. Hoeveel slangen van dezelfde lengte zijn er eigenlijk nodig om alle verschillende woorden in een bepaalde dimensie te maken, zoals de twee (driedimensionale) slangen 000, 010, 011, 001 en 100, 101, 111, 110? De slangen mogen geen woorden gemeenschappelijk hebben.
Er was alleen bekend dat zulke ‘overdekkingen’ bestaan, maar een concrete constructie voor een willekeurige dimensie was nog niet bekend. Haryanto bracht daarin verandering: hij bewees dat elke lijst van 2^n-woorden kan worden overdekt met 2^{m-1}-slangen van dezelfde lengte, waarbij m bepaald wordt door te kijken tussen welke machten van twee n in ligt: 2^{m-1} < n < =2^{m}. Zodoende zijn er in het voorbeeld met de driedimensionale slangen twee slangen nodig van lengte 4.
Deze slangenoverdekkingen kunnen gebruikt worden voor efficiëntere codes. Het is namelijk een groot voordeel dat alle mogelijke woorden gebruikt kunnen worden. Haryanto verwacht dat zijn werk in de toekomst toepassingen zal vinden: “Er zijn zoveel toepassingen voor gewone slangencodes, dat ook deze overdekkingen nuttig zullen zijn. Maar ze zijn gloednieuw. En er zit altijd enige tijd tussen een wiskundige ontdekking en de praktische toepassing.”
De ‘slangencode’ dankt zijn naam aan een meetkundige interpretatie. Als je een kubus tekent en de hoekpunten binair nummert, dan vind je de slangencode door als een slang langs de ribben te kronkelen, met inachtneming van een spelregel: steeds als je op een nieuw hoekpunt aankomt, dan moet je het vorige hoekpunt en alle buurpunten daarvan als onbruikbaar markeren.


Comments are closed.